記入例

　　たけき　だ　　ひでと

　武　木　田　　秀　人

　博士（工学）

　平成１８年３月２４日

学位授与の根拠法規　学位規則第4条第1項

研究科，専攻の名称　東北大学大学院工学研究科（博士課程）機械電子工学専攻

　粒子モデルによる低温磁化プラズマの研究

　
指導教員等は省略

博士論文内容要旨

第1章　緒言

　ドライプロセスと呼ばれるプラズマを用いた半導体製造法は，電子デバイスの作成に欠かせない工程である．プラズマプロセスではさらに微細で効率的な加工を行うために低ガス圧下においても高密度であるプラズマ源が必要とされている．さらに高い歩止まりを確保するためにウエハー寸法は増大し，装置も大型化する傾向にある．このような要求から，プラズマ源は空間的にイオン密度が均一である必要がある．このようなプラズマの閉じ込め方法として注目されているのが，磁場を印加してプラズマを閉じ込める手法である．磁場を印加することにより，電子が磁力線に巻き付いて回転運動をするために壁面に入射して損失されるまでの時間が長くなり，結果として低圧力で高密度なプラズマを生成できる．プラズマに磁場を印加する方法の例としては外部磁場を用いる手法と誘導磁場を用いる手法が存在する．外部磁場を印加する手法として，近年，注目され出したのが多極磁場を有するプラズマ反応器である．この手法は非常に効果的であるが, 装置形状が複雑になるという欠点もある．

低圧力，高密度プラズマの代表ともいえる誘導結合プラズマ(Inductively Coupled Plasma; ICP)は外部アンテナに高周波電流を加えることによって, 誘導電磁場を発生させ，プラズマを生成する装置である．ICPでは電極を装置内に挿入しないので異物混入の心配が無い．また，ウエハーに独立してバイアス電圧を加えることによって，プラズマの生成とは独立してウエハーに入射するイオンのエネルギー分布(IED)を制御することができるので，エッチングを始めとするプラズマプロセスに広く用いられている．

従来，半導体製造装置の設計にさいし，必要な種々のデータは実験によって求められてきた．さらなるコスト削減と開発時間短縮の点から高度な数値シミュレーション技術の開発が必要とされている．磁化プラズマについても流体モデル，粒子モデルやハイブリッドモデルを用いた研究が行われている．しかしながら，プラズマを連続体と仮定して解析する流体モデルは，低ガス圧下では成立が危ぶまれる．これに対して粒子モデルは，電子，イオン，ラジカル，分子などの運動と衝突をBoltzmann方程式とMaxwell方程式を基礎方程式として解析していくために，低気圧下においても適用できる．また流体モデルでは得ることのできない速度分布関数やエネルギー分布関数を得ることが出来る．

以上から本論文では低圧力高密度プラズマである磁化プラズマを対象に，PIC/MC 法(Particle-in-Cell/Monte Carlo 法)を適用してプラズマ構造を解明していく．前半は外部磁場である多極磁場が印加されているプラズマ反応器を対象とする．放電ガスについてはプラズマ生成に広く用いられている希ガスであるアルゴンとし, 放電構造への多極磁場の影響を中心に解析する．後半は磁場の変化により電場が誘起され，この電場による電子加速によってプラズマが生成される誘導結合プラズマを対象に，放電構造とともに中性ガス及びラジカルの流れも解明することを目的とする．放電ガスとしてはアルゴンとともに絶縁膜であるSiO₂酸化膜のエッチングに用いられているCF₄(carbon tetrafluoride)ガスを対象とする．

第2章 軸対称プラズマの解析における局所的重み因子の導入

局所的重み因子を軸対称系のプラズマ解析に導入した．従来の軸対称系のプラズマの解析において，等間隔グリッドを用いた場合には，セルの体積差から中心部のセルに入るシミュレーション粒子数が減少するために，電荷密度が非物理的ゆらぎを起こし，計算が暴走することが問題となっていた．これを避けるために不等間隔セルを用いるのが一般的であるが，その際には差分解の誤差が問題となっていた．

本章ではこのような問題を解決するため，局所的重み因子を軸対称系のプラズマ解析に導入した．局所的重みではシミュレーション粒子の重みをセルごとに変化させることより，中心部のセルにおいても十分な数のシミュレーション粒子を確保することが出来る．この考え方が問題無く用いられることを示すために2円筒間における直流放電をモデリングし，従来の手法と計算結果が一致することを確認した．さらにこの手法を用いることで中心部の電荷密度のゆらぎを取り除くことに成功した．

第3章 多極磁場を有するプラズマ反応器の２次元解析

多極磁場のプラズマ閉じ込め効果についてPIC/MC法を用いた解析を行なった．低温プラズマにおいて多極磁場の効果がはじめて示された装置を単純化し，中心軸上の加熱されたフィラメントからの電子放出により放電が維持される熱陰極放電をモデリングする．背景ガス圧力，磁場の強さ，磁極数を変化させた系統的解析を行い，多極磁場がプラズマに及ぼす影響を明らかにした．プラズマ密度は5 mTorr以下の圧力域において，約１桁増加する．図1は磁場強度0.1 Tにおける装置内の電子密度である．磁極付近にピークを持つ空間構造が明らかにされた．さらには磁場を印加した場合には，プラズマ電位が負の値を持つことが明らかにされた．図2に電子密度n_eの増加率のガス圧力依存性を示す．中心から放出された高エネルギー電子の平均自由行程が放電長さ(ここでは装置の半径)よりも長いような低圧力の条件の場合に，プラズマ閉じ込めの効果が大きいことが分かった．また閉じ込めのための最適な磁極数が存在することを明らかにした．

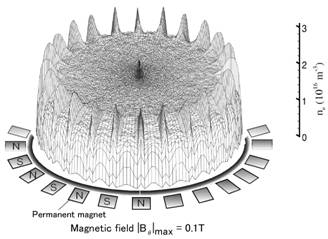
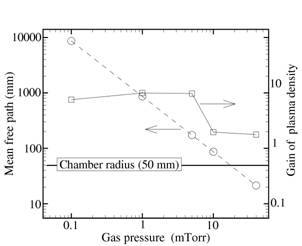
　図１　電子密度（磁場強度0.1 T) 　　　　　　　図2　電子密度の増加率と電子の

平均自由行程の圧力依存性

第4章 多極磁場を有するプラズマ反応器の3次元解析

第3章の解析を発展させ，軸方向に有限の装置形状を考え，多極磁場を有するVHFプラズマ反応器の3次元解析を行った．装置形状としては2次元解析の際と同様に円筒状であり，軸方向に平行平板型電極が存在する．3次元モデルでは電極面積が有限であり，装置壁が存在することから放電が非対称となって，自己バイアス電圧が発生する．プラズマ構造に対するガス圧力と多極磁場の影響を解析した．プラズマ密度は，40 mTorr以下の圧力域において約１桁増加する．また磁場無しでは放電を維持することの出来なかった10 mTorrにおいても放電を維持することが出来た．2次元の解析の場合と同様にプラズマ密度は壁面付近でピークを持ち，このピークの存在により，電極へのイオンフラックスの一様性が悪化する．一方，電極に入射するイオンのエネルギー分布関数(IED)には磁場は大きな影響を与えない．2次元の場合と比較すると，高エネルギー電子の生成場所が装置全体に広がるために，さらに高い圧力域においても磁場が有効であることが示された．

第5章 ウエハーにバイアスを印加した誘導結合アルゴンプラズマの解析

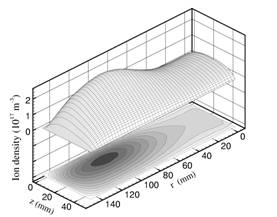
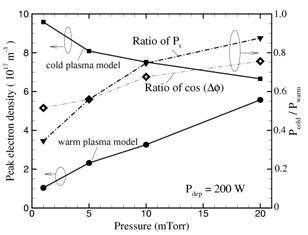
誘導結合アルゴンプラズマについて，アンテナ電流と誘導プラズマ電流による電磁場に加えてウエハーバイアスによる静電場を考慮した数値解析コードを開発し，無衝突加熱の効果を評価した．図3に誘導結合プラズマ中のイオン数密度分布を示している．図4には電子数密度の圧力依存性を示している．このとき，吸収電力の計算では，無衝突加熱を考慮した電流密度(warm plasma current)と無衝突加熱の効果を無視した電流(cold plasma current)の双方において，吸収電力を一定に保ち，圧力を変化させた．その結果，無衝突加熱を考慮した場合には，圧力に対するプラズマ密度の変化が実験結果と定性的に一致した．無衝突加熱を考慮したP_warmを一定にした解析では圧力が低い場合ほど，無衝突加熱の割合が大きくなり，衝突加熱のみを考慮した吸収電力P_coldを一定にした解析では，低圧のさいに電子密度を過大評価してしまうことを示した．

またウエハーに印加したバイアス周波数およびバイアス電圧をパラメータとした解析を行い，実験や理論解と比較した．結果は実験や理論で得られた解析解を再現し，本モデルの信頼性を確認した．


図3　装置内のイオン密度	図4　電子数密度の圧力依存性

第6章 ウエハーにバイアスを印加した誘導結合CF₄プラズマの解析

誘導結合CF₄プラズマを対象に，放電構造のガス圧力及び吸収電力に対する依存性を解析した．すなわち，荷電粒子密度比および空間密度分布の変化を明らかにした．また，バイアス周波数のIEDに対する影響を明らかにした．図5はバイアス周波数が2 MHzの時の基板に入射するイオンのエネルギー分布関数である．低周波数のためにイオンはシース電位の変化に追随し，IEDはダブルピーク構造を持つ．図6に，シミュレーションで得られたピーク幅ΔEを，バイアス周波数とイオンの質量に依存するパラメータS_iを用いて過去の実験から得られた経験式と比較して示す．点で示されたシミュレーション結果は理論式とよく一致し, シミュレーションの信頼性が確かめられた．　

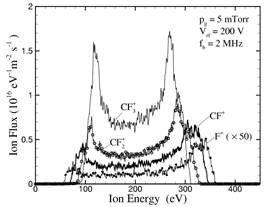
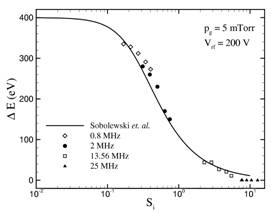
　図 5 　2 MHzの場合のIEF. 図6 　ΔE vs. S_i

第7章 CF₄/Ar系の誘導結合放電の解析

　第5章と第6章のモデルを発展させ，CF₄/Ar系混合ガスの誘導結合放電を全圧を固定し，ガスの混合比の影響を解析した．すなわち混合比による電子密度の空間分布，電子のエネルギー分布関数の変化を明らかにした．

第8章 CF₄誘導結合プラズマにおけるガス流れの粒子モデル解析

　ICP装置内の中性ガス流れ場をDirect Simulation Monte Carlo (DSMC)法によって調べ，装置内におけるラジカルの流れ場を明らかにするとともに，エッチレートの予測を行った．第6章のプラズマ解析で得られたラジカルの生成レートを用いて装置内にCF_xラジカルを発生させた．CF₄およびCF_xラジカルの温度と密度は壁面の温度に影響された空間分布を持つことが明らかになった．ガス圧力や吸収電力を変化させた場合の数密度の定性的な変化は，以前に行われた実験やグローバルモデルの結果と定性的に一致した．また，表面反応確率を増加させるとエッチ生成物がラジカルのウエハーへの入射を妨げるためにエッチングレートが増加せず，エッチングレートの一様性も悪化することを明らかにした．

第9章 ガス流れとプラズマの粒子モデルによる連成解析

第6章と第8章の解析を発展させ，プラズマと流れを連成させた解析モデルを構築し，中性ガスの密度分布と流れがプラズマに与える影響を逐次近似により解析した．プラズマ解析の後，流れ解析に移るにはラジカルの生成レートを受け渡し，流れ解析からプラズマ解析へ移る時は，母ガスであるCF₄分子の数密度の分布を衝突の衝突確率の決定に利用する．流れ場解析とプラズマの解析を交互に行って行き，流れとプラズマ双方の状態が収束するまで解析を繰り返し，それぞれの影響を逐近似的に考慮していく．図7に連成解析によって得られたr, z平面でのCF₄の密度，電子数密度，そしてｒ, θ平面でのエッチング作用物質であるCF₂のウエハー面での数密度，CF₂のフラックスにより求められたエッチレートの分布を示す．連成解析によって背景気体CF₄の密度の空間的非一様性が荷電粒子密度の分布に影響を与えることを明らかにした．

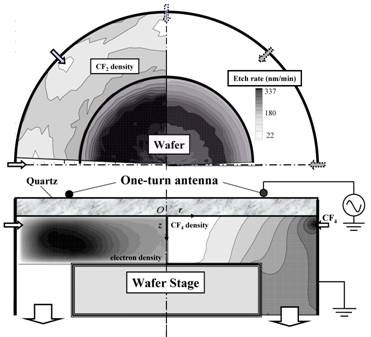
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　図7　 CF₄密度，電子密度，CF₂密度，エッチレート

第10章 結　論

　各章で得られた結果の総括を行った．

　本論文ではプラズマプロセスに用いられている磁化プラズマの中で，多極磁場を有するプラズマと誘導結合プラズマについて，プラズマだけでなく中性ガスの流れをも含めた粒子モデルによるシミュレーション法を構築した．これを用いて装置内の電磁場，荷電粒子の数密度分布，中性ガス流れ場を求め，プラズマの構造を明らかにし，磁化プラズマ装置の設計に有用な知見を得ることが出来た．